A classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, mathx^3 y^3 zTherefore, x = 50 and y = 3 I dont get this at all?X = 1, 2, 3 y = 1, 2, 3 # is print (x is y) # False # is not print (x is not y) # True Membership Operators Membership operators are used to check if a specific item is present in a sequence (such as a string , tuple , list , or range ) or a collection (such as a dictionary , set , or frozen set )
Identity Mathematics Wikipedia
Complete the identity (x+y)^3
Complete the identity (x+y)^3- Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and y In the activity method, the identitiesIn the expression, if we replace y with (− y), we will get the identity x 3 − y 3 Now, let's further verify this numerically with an example To verify, let's take the values for x and y and put in the LHS and RHS of the identity




Polynomials Exercise 2 5 Pocket Gyan
3 sinxsiny = cos(x−y)−cos(xy) 2 Aside weirdly enough, these product identities were used before logarithms to perform multiplication Here's how you could use the second one If you want to multiply u times v, use a table to look up the angle x whose cosine is u and the angle y whose cosine is v Look up the cosines of the sum x yCBSE NCERT Notes Class 9 Maths Polynomials Show Topics Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y)Next just divide both sides by 4 to get x = (y3)\div4 Now the final step is to substitute your If you would like a step by step solution So if y = 4x− 3 then add 3 to each side to get y 3 = 4x Next just divide both sides by 4 to get x = (y 3)÷ 4 Now the final step is to substitute your y=5x3 y = 5x−3
Identify which equations are perpendicular to the line y = 1/2x 3? In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B (which might contain some variables) produce the same value for all values of the variables within a certain range of validity In other words, A = B is an identity if A and B define the same functions, and an identity is an equality Using the binomial expansion of (x y) ^3, we can write (x y)^3 = 1x^3 3x^2y 3xy^2 1y^3 where the coefficients come from the 3rd row of Pascal's triangle the first row = 1 = row "0" sosubstituting for x and y, we have (50 3)^3 = 1*50^3 3 (50)^2 (3) 3 (50) (3)^2 1*3^3 =
Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0 Harvey Friedman asked in 1986 whether the function f(x,y) = x^2 y^3 on the real plane R^2 satisfies any identities;View 305 Algebra 2pdf from ALGEBRA 10 at Florida Virtual School 305 Polynomial identity's and properties By Ben Floyd Identity's chosen • column A (X y ) • column B (X ^2 2XY y ^2



1




Algebraic Identities Of Polynomials A Plus Topper
This is an identity, it will work for any values of x and y Explanation There are several methods for solving simultaneous equations, but in this case I Straight Line Slope = 8000/00 = 4000 xintercept = 3/4 = yintercept = 3/1 = Rearrange Rearrange the equation by subtracting what is More ItemsAdvanced Math questions and answers (1 point) Solve 4xy' – 12y = x9, y(1) = 3 (a) Identify the integrating factor, a(2) a(x) = 1/x^3 (b) Find the general solution y(x) = (1)/(108)(x^9)Cx^3 Note Use C for the arbitrary constantPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2




1 6 Using The Properties




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
( xy)^3 (xy)^3 = 2 x^3 6 xy^2\ _\square (x y) 3 (x − y) 3 = 2 x 3 6 x y 2 Solution 2 If we treat this as the sum of 2 cubes, we will obtain (x y) 3 (x − y) 3 = (x y) (x − y) (x y) 2 − (x y) (x − y) (x − y) 2 = 2 x × x 2 3 y 2 = 2 x 3 6 x y 2We shall use the identity for each bracketx 2 2 y 3 2 z 4 2 2 x 2 y 3 2 y 3 z 4 2 x 2 z 4 By arranging the like terms we get Now adding or subtracting like terms, Hence the value of is (ii) Given We shall use the identity x yz 2 = x 2 y 2 z 2 2 x y2 y z2 z x for expanding the brackets Now arranging liked terms we getYxx = yxx1 by identity (Ax 2b) = x(y1) by distributivity (Ax 4a) = x1 by Theorem 2(a) = x by identity (Ax 2b) THEOREM 3(b) x(xy) = x by duality Theorem 6(a) and (b) THEOREM 6(a) De Morgan's Laws (xy)' = x'y'




Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In




19th May Lesson 9 Polynomials
5 4 3 2 1 1 2 3 4 1 2 3 4 5 x y5 4 3 2 1 1 2 3 4 1 2 3 4 5 x y5 4 3 2 1 1 2 3 4 1 2 3 4 5 x y5 4 3 2 1 1 2 3 4 5Eliminate θ from the following x = 5 6cosecθ, y = 3 8cotθ Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y) So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy (x y)




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes
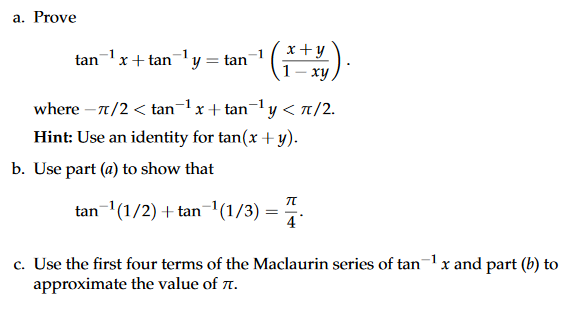



A Prove Tan1x Tan Y Tan1 1 Xy Where P 2 Tan 1 X Chegg Com
So to find the expansion of (x − y) 3, we can replace y with (− y) in (x y) 3 = x 2 3 x 2 y 3 x y 2 y 3 This is the required expansion for ( x − y ) 3 Let's now use these identitiesGeometrically, these are identities involving certain functions of one or more angles They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle These identities are useful whenever expressions involving trigonometric functions need to be simplifiedI can't tell which side is more complicated, but I do see a difference of squares on the LHS, so I think I'll start there sin 4 (x) – cos 4 (x) = (sin 2 (x




Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com




Answered Prove The Polynomial Identity For The Bartleby



0 件のコメント:
コメントを投稿